吾教吾学
对一道数学竞赛试题解法的探讨
□界首市逸夫第一小学  邢  浩
    拜读《小学数学教师》2009年第12期乐家骏老师的《不等式在解题中应用》时，颇感受益匪浅。特别对乐老师解题方法之精彩，啧啧称赞，以致爱不释手。在文后，乐老师给读者提供了5道练习题，其中第2题是：“小凤在计算一道求七个自然数的平均数（得数保留两位小数）时，将得数的最后一位弄错了，她的错误答案是21.83。正确答案应是多少？”（福州市小学生“迎春杯”数学竞赛试题）在练习题后，乐老师给我们提供的答案是这样的：“正确答案在21.80与21.89之间。设正确答案为x，则有21.80≤x≤21.89，各项乘以7得152.6≤7x≤153.23。因为7个自然数的和为整数。所以，7x=153，x≈21.86，正确答案应是21.86。”
    作为数学教师，我平时也喜欢演算竞赛题。在享受乐老师这道竞赛题解法时，有一种追慕先贤的冲动，现奉与大家，以求斧正。
    解法一：大胆猜想，估值判断
    小凤的答案21.83只是错在了百分位，前面的21.8仍是正确的。21.8×7=152.6，说明7个自然数的和比152.6多一点儿，而且是个自然数。由于百分位上的数字与7相乘的积很小，自然对7个自然数的和的影响也很小。因此可以断定7个自然数的和是153，153÷7≈21.86，正确答案是21.86。
    解法二：巧用规律，直接判断
    小凤的答案21.83只是错在了百分位，前面的21.8仍是正确的。21.8×7=152.6，由于7个自然数的和也是个自然数。所以可断定这7个自然数的和是一个三位数。假设这个三位数是，可列出如下除法竖式。

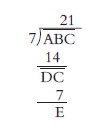
    说明：1.由于商里21.8是正确的，所以2应商在十位数字B的上面。2×7=14，   －14的差只能是一位数，假设为D，且D＜7。（初等数论证中带余数除法定理表述为：“若a、b是给定的两个整数，且b≠0，则一定存在唯一的一对整数q和r，满足a=bq+r，0≤r＜｜b｜）
    2.把个位数C移下来，组成两位数   ，根据题意   ÷7的商是1，1写在被除数中C的头上。1×7=7，   -7的差只能是一位数，假设为E，且E＜7。（理由同上）
    这时可知：E必为1、2、3、4、5、6中的某一个数。由于1÷7=0.142857、2÷7=0.285714、3÷7=0.428571、4÷7=0.571428、5÷7=0.714285、6÷7=0.857142，而商的十分位上是8，所以可以确定E=6，商应该是21.857142。因为题目中要求保留两位小数，所以，正确答案应是21.86。
    解法三：除法竖式，推理判断
    如上面第二种解法：当    ÷7=21……E，且E＜7（理由同上）时我们可以继续往下除。（竖式略）
    说明：1.在商的个位1后面点上小数点，再在余数E的后面补成为两位数，  ÷7根据题意应上8，8写在商的十分位上。7×8=56，（E只能是6）   -56的差只能是4（理由同上）。
    2.在4后面补0成为40，40÷7=5……5，所得商的5应写在商的百分位上。在余数5的后面补0成为50。50÷7=7……1，所以商的千分位上应该是7。
    这时可以得出：    ÷7=21.857……，用“四舍五入”法保留两位小数应该是21.86。所以正确答案应是21.86。
    以上浅见，希望对您能有些许帮助，若能因此而抛砖引玉，将使笔者喜出望外。