特别推荐
巧用模型解答排列组合问题
□合肥百花中学(寄宿制校区)  胡中祥
排列组合问题是富有趣味的一类题目，因为不同的人往往有不同的思路。比如贝特朗的几何概率悖论：在圆内作一条弦，求其弦长超过该圆的内接正三角形边长的概率。不同人有不同的解答，且都合理，趣味无穷。
题文：如图4×4的方格，求A到D的最短走法（一步可以走一格、两格或三格，拐弯可连续。如到C点可以一步一格走两步，也可一步拐弯走两格到达）。
笔者认为要想排列组合不出错，必须思路清晰，最好的方法就是归纳模型，套用模型去解。比如捆绑、插空、整数解、路灯、街道、楼梯、错拿、圆桌、涂色等。下面我介绍如何用街道和楼梯模型秒破这类题。

街道模型
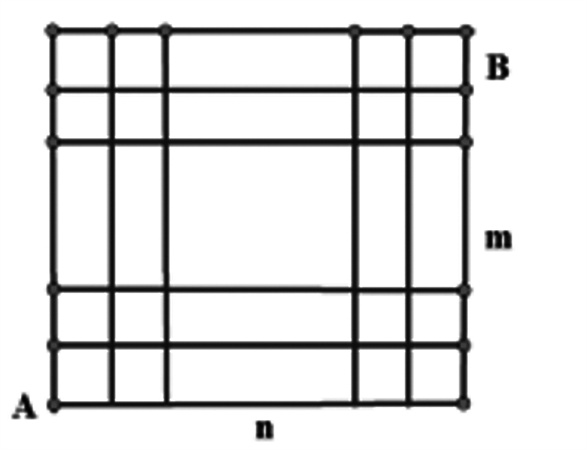
如图所示，m×n的方格，从A走到B，一步走一格，要使总的步数最少，走法有多少种？
分析：考虑步数最少的走法时，每一步只能往上或往右走，从A到B一共要走m+n格，其中m个向上，n个向右，考虑在m+n个位置中选取n个向右，则剩下均向上，这样就完成最短的走法，有Cm+n=Cm+n种走法。

楼梯模型
一层楼有n级阶梯，可一步跨一级或两级，有多少种走法？
很多人用不定方程的整数解，然后“插空”解，这样可以，但是当数字大、可跨级数多时，极易出错，难以操作。笔者介绍一种类似斐波那契数列的构造法，假设到达第n级阶梯的方法有an种，可知a1=1，a2=2，a3=3。最后一步，可从第n-1级走一级，也可从第n-2级走2级，到达第n级，故an=an-1+an-2(n≥3)，这样an的通项就可求出，在此不阐述了。
若一次可跨一、二、三级，易知b1=1，b2=2，b3=4，bn=bn-1+bn-2+bn-3(n≥4)。
据此可以已知推到n级阶梯，可以走一级、二级……m级的走法，常用跨一、二级记为｛an｝，跨一、二、三级记做｛bn｝，如下：
一级或二级
｛an｝：a1=1，a2=2，a3=3，a4=5，a5=8，a6=13，a7=21，a8=24，a9=55，a10=89……an=an-1+an-2(n≥3)
一级或二级或三级
 ｛bn｝：b1=1，b2=2，b3=4，b4=7，b5=13，b6=24，b7=44，b8=81，b9=149，b10=274……bn=bn-1+bn-2+bn-3(n≥4)
例题
例题1：某城市东西5条街道，南北6条街道，一个人在A点，现在他想到B点购物，则最短走法有多少种？
分析：C11=462种。
例题2：一堆火柴有13根，每次可以取出1到3根，有多少种方法取完？
分析：类比一个12级楼梯，一级放一根火柴，一次跨几级就捡几根，答案是b12=927种。
例题3：小区一栋小矮层，共三楼，每层15个台阶。一个人前三分之一一步可跨一个、两个或三个台阶，后三分之二一步可跨一个或两个台阶，一共有多少种走法？
分析：三楼共2×15=30个台阶，前10个走完有b10种走法，后20个走完有a20种走法，故共有b10×a20=274×10946=2999204种走法。
例题4：将文章开篇题目条件改为：一步可以走一格或两格。
分析：分成两步考虑：
1：A到D最短走法为C8=70条。
2：将每一条看作一8级楼梯，则有a8=34故有C8a8=2380种。
注1：此题有很多错误答案，其中有两个经典错误。
   一：列举叠加。
   二：对称相乘。
注2：3×3的网上和资料上也有很多错误答案流传，现将正确的列出。
一步：C6=20种。
一步或两步：C6a6=260种。
一步、两步或三步：C6b6=480种。
注3：由此可以算出开篇那道题目答案：C8b8=70×81=5670种。
最后我原创一道题来结束此文：

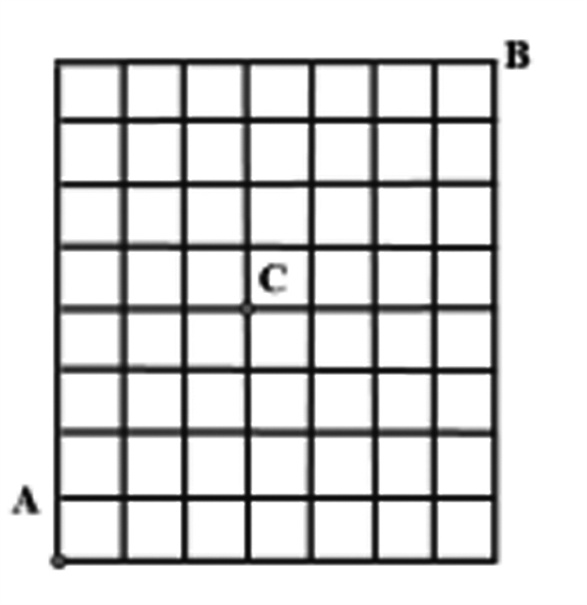
有一天笔者在毛坦厂镇规划局见到镇规划图大致如图所示，现在我在A处，要到毛坦厂中学的B处上课，想路上经过C处快递点取一个快递，在到C之前可以一步跨1个、2个或3个方格，拿到快递后就一次跨1个或2个方格了，则到达学校的最短走法有多少种？
答案： C7b7×C8a8 =3665200。